Spørgsmålet
Kære Peter
Hvad giver lyden når man fløjter?
James.
Det korte svar
Når luft bevæger sig hurtigt forbi en skarp kant (som f.eks. spidsede læber eller kanten i en fløjte), skabes turbulens som giver anledning til trykbølger.
Geometrien af systemet (altså munden, fløjten, eller hvad det nu er der fløjter) bestemmer, hvilke bølgelængder der forstærkes og hvilke der udslukkes, sådan at kun nogle bestemte toner høres.
Det lange svar
Turbulens og trykbølger
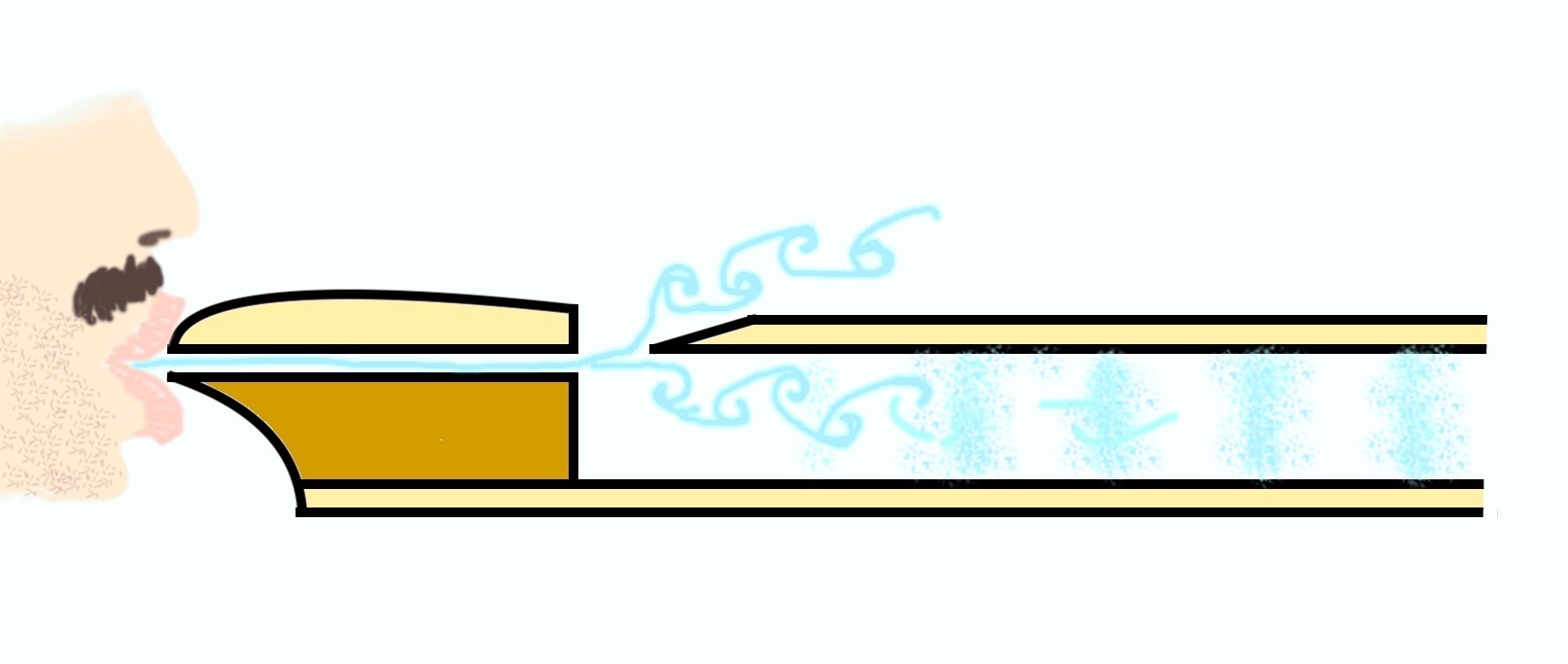
Fysikken bag lyden af et fløjt er ikke helt triviel og afhænger af, præcis hvad der er der fløjter, f.eks. om det er et fløjt fra læberne, en blokfløjte, fløjten på en vandkedel, et pust henover en flaske, osv.
Men grundliggende er mekanismen, at luft-flowet henover en kant bliver turbulent. Det vil sige, at det ikke flyder afsted i en jævn strøm, men hele tiden ændrer retning på tværs af udbredelsesretningen.
Disse bevægelser frem og tilbage skaber små over- og undertryk, der udbreder sig afsted gemmem luften med lydens hastighed — for dét er nemlig lige akkurat hvad lyd er; skiftende trykbølger der bevæger sig gennem luften.
Lyden af en fløjte
Turbulens er temmelig kaotisk, så luftbølgerne skabes med forskellige bølgelængder, og dermed frekvenser. Sammenhængen mellem en bølges bølgelængde \(\lambda\) og frekvens \(f\) er givet ved \(f = c / \lambda\), hvor \(c\) er lydens hastighed. Altså, jo kortere bølgelængde, jo højere frekvens, dvs. jo lysere tone.
I en blokfløjte bevæger bølgerne sig langs fløjten fra mundstykket og ud mod enden. Når de møder det "frie" rum, fortsætter bølgerne ud i rummet, men samtidig reflekteres bølgen tilbage langs fløjten. Denne reflektion skyldes, at når et lille overtryk forlader fløjten, efterlades et lille undertryk, som så udbreder sig tilbage gennem fløjten.
Derved bevæger bølger med flere forskellige bølgelængder sig frem og tilbage i fløjten. Når to bølgetoppe eller -dale mødes, forstærker de hinanden, mens når en top og en dal mødes, udslukker de hinanden. Dette kaldes interferens.
Grundtone og overtoner
Fordi fløjter normalt er åbne i begge ender, vil et overtryk reflekteres som et undertryk i begge ender. Det betyder, at bølgelængder som "passer" til fløjtens længde \(L\) med et helt antal halve bølgelængder forstærkes, mens alle andre udslukkes. Dermed skabes stående bølger med bestemte bølgelængder.
Den længste bølgelængde der passer til fløjten, \(\lambda = 2L\), giver den dens dybeste tone, grundtonen. Lidt kortere bølgelængder udslukkes, men hvis de har en længde på \(\lambda = 1L, \frac{2}{3}L, \frac{1}{2}L\), … forstærkes de Dette giver instrumentet dets overtoner.
For eksempel vil grundtonen af en fløjte på en halv meter have en bølgelængde på \(\lambda =\) 1 m. Da lydens hastighed ved normalt atmosfærisk tryk og temperatur er \(c =\) 340 m/s, bliver frekvensen \(f = c / \lambda = \) 340 Hz, hvilket ligger sådan ca. midt mellem en E- og en F-tone.
(Dette er ikke helt korrekt, dog: I virkeligheden reflekteres trykbølgen lige lidt udenfor fløjtens munding, ca. 0.6 gange fløjtens diameter. Så hvis fløjten er 2.5 cm tyk, fås 330 Hz, hvilket er et næsten rent E.)
Ved at lette fingrene fra hullerne i fløjten, gøres den effektivt set kortere, hvilket så giver lysere tonere.
Lyden af en klarinet
Fløjter har en åbning henne ved munden, så et overtryk reflekteres som et undertryk, og omvendt, i begge ender. Andre instrumenter, f.eks. klarinetter og oboer, er kun åbne i den ene ende, så i mund-enden reflekteres et overtryk som et overtryk.
Effekten er, at bølgelængderne bliver dobbelt så lange som fløjten; derfor giver sådan nogle instrumenter dybere toner.
Lyden af et fløjt
Fysikken i et menneskefløjt er lidt anderledes, selvom grundprincipperne er de samme. Her har vi et stort kammer med en lille åbning, hvilket minder lidt om en flaske. Et sådan system giver en såkaldt Helmholtz-resonans, hvor man kan vise, at frekvensen ved normalt tryk og temperatur bliver ca. $$ f = 7260\,\mathrm{Hz}\,\times\,\sqrt{\frac{d}{D^3}}, $$ hvor åbningen og hulrummets diametre \(d\) og \(D\) er målt i cm.
Fløjte-eksperiment
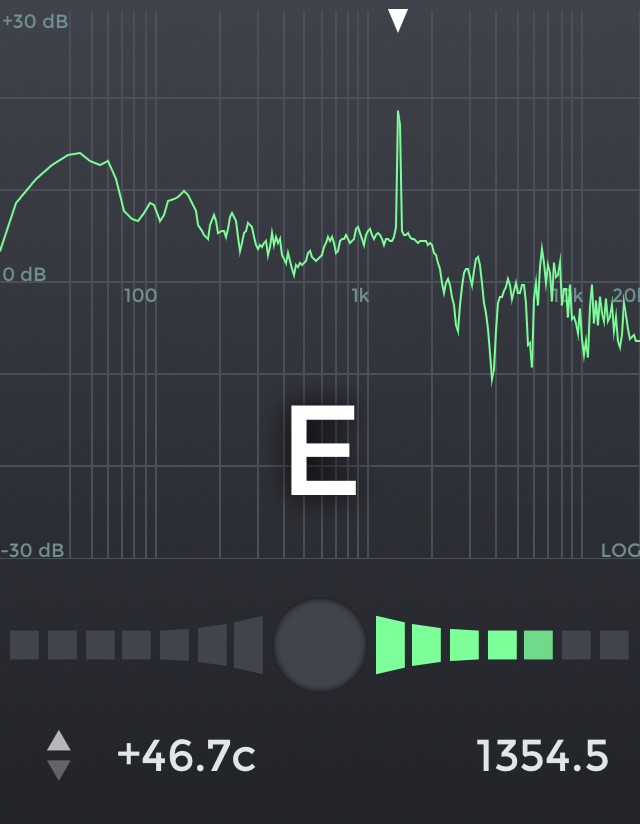
Jeg har lige foretaget følgende eksperiment. Jeg formede munden til et fløjt og målte dybden af min munds hulrum til 2 cm med en tandstik (afstand fra læber til tungen, som afkorter mundhulen), og diameteren af hullet skabt af mine spidsede læber til 3 mm. Ifølge formlen ovenfor skulle frekvensen så være 7260 Hz \(\sqrt{0.3/2^3} \simeq \) 1400 Hz, hvilket er ret tæt på et F.
Ifølge min frekvensmåler var mit fløjt et E ved ca. 1354.5 Hz — blot en halv tone ved siden af :)
Science — it works, bitches!
Bedste hilsener,
Peter