Spørgsmålet
Hej,
Hvis vi forstiller os 2 stjerner, en 1 lysår fra jorden og en 1.000.000 lysår fra jorden. Så vil lyset fra stjerne nr. 2 være red-shiftet mere end nr. 1. Det vil sige at stjerne nr. 2 bevæger sig hurtigere væk, end stjerne nr. 1 gør.
Lyset fra stjerne nr. 2 er 1.000.000 år gammelt, det havde altså den hastighed for 1.000.000 år siden.
Det betyder at for 1.000.000 siden udvidede universet sig hurtigere, end det gør i dag, altså at udvidelsen bliver langsommere og langsommere..!?
Mvh. Lars
Det korte svar
Jeg forestiller mig, at grunden til at du spørger, er fordi du har hørt at Universet skulle udvide sig hurtigere og hurtigere.
Men for det første måler vi ikke den hastighed, galakserne havde da lyset blev udsendt. Vi måler rødforskydningen, og vores teoretiske model af Universet fortæller os så, hvilken hastighed den har, både nu og tidligere.
For det andet bevægede fjerne galakser sig faktisk gradvist langsommere væk fra os i starten, og begyndte først for relativt nyligt at bevæge sig hurtigere igen. Vi tror at grunden er, at tyngdekraften først bremsede udvidelsen op, men at det der kaldes "mørk energi" senere begyndte at accelerere den igen.
Baggrundsviden fra encyklopædien
Få evt. lidt baggrundsviden om rødforskydning i encyklopædien her:
Det lange svar
En lille ændring af dit spørgsmål
De første tre afsnit er tænkt som en baggrund for at besvare dit spørgsmål. Hvis du er utålmodig, kan du skippe dem og gå direkte til svaret i sidste afsnit.
Selvom det ikke har betydning for spørgsmålets "idé", vil jeg allerførst lige ændre lidt på eksemplet. Det er nemlig sådan, at selvom Universet på store skalaer udvider sig, holder tyngdekraften på "lille" skala sammen på det.
Det vil sige at Jordkloden ikke udvider sig, at galaksernes egne stjerner ikke fjerner sig fra hinanden, og at vi endda ikke fjerner os fra vores nærmeste nabogalakser. Andromeda, for eksempel, ligger 2½ million lysår væk, men er alligevel på vej imod os. På endnu mindre skalaer end Jorden holder elektromagnetismen sammen på f.eks. din krop, så du heller ikke udvider dig (hvis du altså har holdt lidt igen med juleanden).
Så tillad mig at ændre spørgsmålet til at betragte to galakser som er hhv. 1 og 2 milliarder lysår væk. Lad os kalde dem G1 og G2.
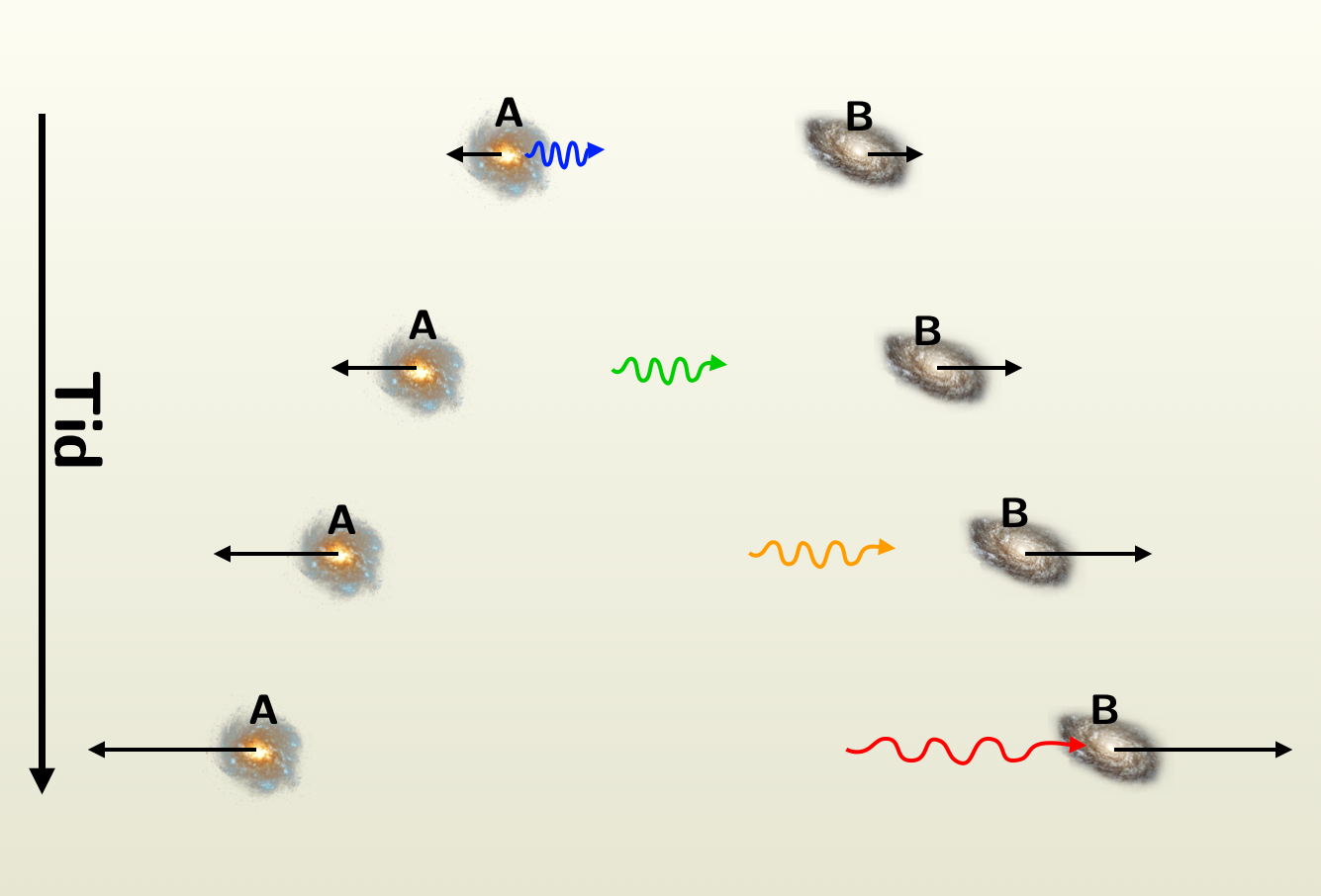
Pga. Universets udvidelse har galakserne fjernet sig fra os i den tid, der er gået siden de udsendte dét lys vi ser. Så lyset har ikke helt brugt 1 og 2 mia. år på at nå os, fordi de var tættere på os i fortiden. Det har brugt lidt mindre tid, men i mellemtiden er galakserne rykket længere væk og ligger i dag hhv. 1 og 2 mia. lysår væk.
Men det er vigtigt at forstå, at det ikke er noget man bare kan se ud af deres "redshift", eller rødforskydning, som vi kalder det på dansk.
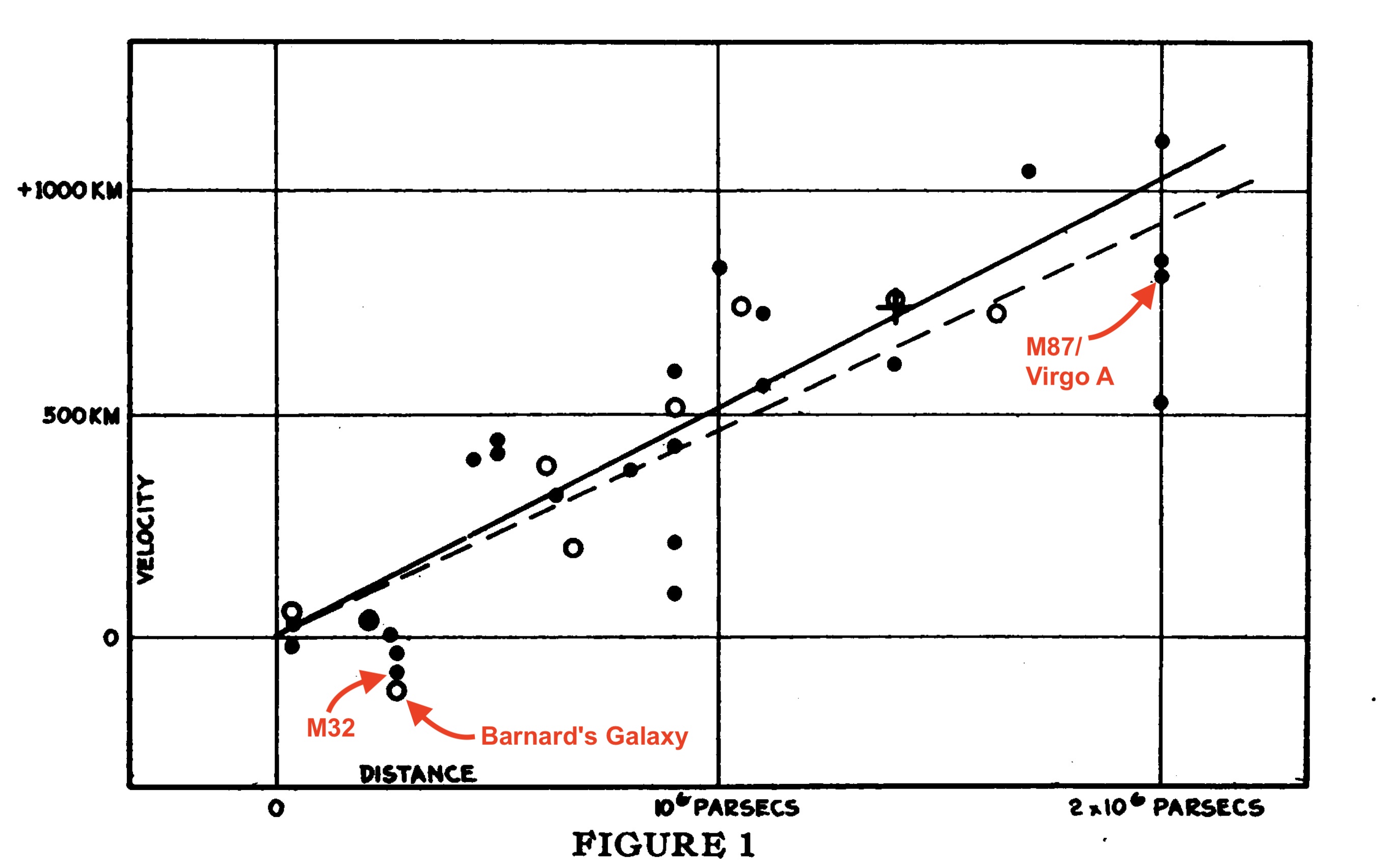
Man kan se, at der er stor spredning i hastighed, og nogle af de nærmeste galakser bevæger sig endda hen imod os (dvs. de ligger nedenunder x-aksen, altså med negative hastigheder). Men generelt er mønstret, at jo længere væk, jo hurtigere fjerner de sig. Edwin Hubble under-estimere dog de fleste afstande, og over-estimerede derfor udvidelseshastigheden med mere end en faktor 7.
Kredit: Edwin Hubble (1929), med mine annoteringer med navne på nogle af galakserne.
En model af Universet
Det vi måler, er hverken en udvidelse, eller en hastighed, eller en alder, men slet og ret rødforskydningen. At koble denne observerede rødforskydning til de andre størrelser kræver først en fysisk model af Universet og dets dynamik. En "model" er i fysik en teoretisk repræsentation af et system, som kan forklare og eventuelt forudsige forskellige fænomener relateret til systemet.
Du er måske bekendt med rødforskydning fra dét fænomen, der kaldes Doppler-effekten: Hvis du måler bølgelængden af noget lys, som bevæger sig væk fra dig, vil du finde, at det er blevet mere langbølget, dvs. rødere. Omvendt vil lyset fra et objekt, der bevæger sig hen imod dig blive blåforskudt. Vi bruger bl.a. dette til at måle hastigheder af nære stjerner (så kan vi f.eks. se om de har planeter omkring sig, som hiver dem lidt frem og tilbage).
Doppler-effekten er en forudsigelse af den teori vi kalder "den specielle relativitetsteori" (eller "SR"). Men det er ikke det vi tror der sker med fjerne galakser.
Den bredest accepterede model af Universet er den såkalde ΛCDM-model (udtales "Lambda-CDM"), som bygger på den generelle relativitetsteori (eller "GR"), nogle få og rimelige antagelser, og et antal observerede fysiske parametre.
I korte træk siger GR, at selve rummet kan udvide sig, trække sig sammen, og forme sig vilkårligt, alt efter hvor og hvor meget det indeholder af forskellige former for energi.
Præcis hvordan vores Univers opfører sig, afhænger dermed af forskellige parametre, og hele den gren af fysikken, som kaldes "kosmologi" går i det store hele ud på at bestemme disse parametres værdier observationelt, så præcis som muligt.
Når vi så måler, at galaksernes lys er rødforskudt, og at rødforskydningen er større, jo længere væk de ligger, passer det ind i en model der siger, at Universet er i gang med at udvide sig.
I denne model skyldes galaksernes rødforskydning derfor ikke at de bevæger sig væk fra os, men derimod at selve rummet udvider sig. Det er altså ikke helt det samme, som når man måler bølgelængden af lys, der bliver udsendt fra en objekt, som bevæger sig ift. os. Galakserne ligger (forholdsvis) stille i rummet, men selve rummet udvider sig, og derfor øges afstanden mellem galakserne. Derfor fortæller rødforskydningen os ikke bare, hvilken hastighed galakserne havde, dengang de udsendte lyset.
Mere præcist fortæller rødforskydningen os forholdet mellem Universets størrelse i dag og dengang lyset blev udsendt. Hvis vi f.eks. måler en foton til at have en bølgelængde på 244 nanometer, men vi ved fra atomteori at den har været udsendt med bølgelængden 122 nanometer, så ved vi at den blev udsendt dengang Universet var halvt så stort som i dag.

Andre modeller
Det lyder måske lidt vilkårligt. Altså, der kunne vel også være andre modeller, som ville gøre at galaksernes lys var rødforskudt. Og jo, det kan der. Men rødforskydningen er bestemt ikke den eneste grund til, at vi tror at ΛCDM er en god beskrivelse af Universet. En lang, lang række af forskellige observationer passer rigtig, rigtig godt ind i de forskellige teoretiske aspekter af ΛCDM. Mange andre modeller har været fremsat gennem de sidste hundrede år, men de fleste er endt med at blive modbevist, og de resterende kræver mere og mere fintuning, efterhånden som vi får flere og bedre data.
Den simplere antagelse, nemlig at rummet ikke udvider sig, men at galakserne fjerner sig fra hinanden ved at bevæge sig gennem rummet, og dermed have en helt almindelig Doppler-forskydning, har selvfølgelig også været betragtet. Men for det første er sådan et statisk univers simpelthen ikke kompatibelt med GR, og vi ville derfor være nødt til at finde en ny forklaring på alle de fænomener, som GR kan forklare. For det andet passer vores målinger af sammenhængen mellem galaksernes rødforskydning og deres afstande meget, meget bedre med GR end med SR.
Se selv figuren på højre side (eller nedenfor, hvis du læser på en lille skærm).
Mere eksotiske hypoteser har også været fremsat, f.eks. at galakserne ikke fjerner sig fra hinanden, men at lyset af en eller anden grund bliver "træt" undervejs og mister energi. Men man har ikke kunne finde nogen plausibel grund til, at det skulle miste energi, og da der er andre fænomener, som det ekspanderende Univers kan forklare, men som træt-lys-hypotesen ikke kan, er man gået væk fra dén.
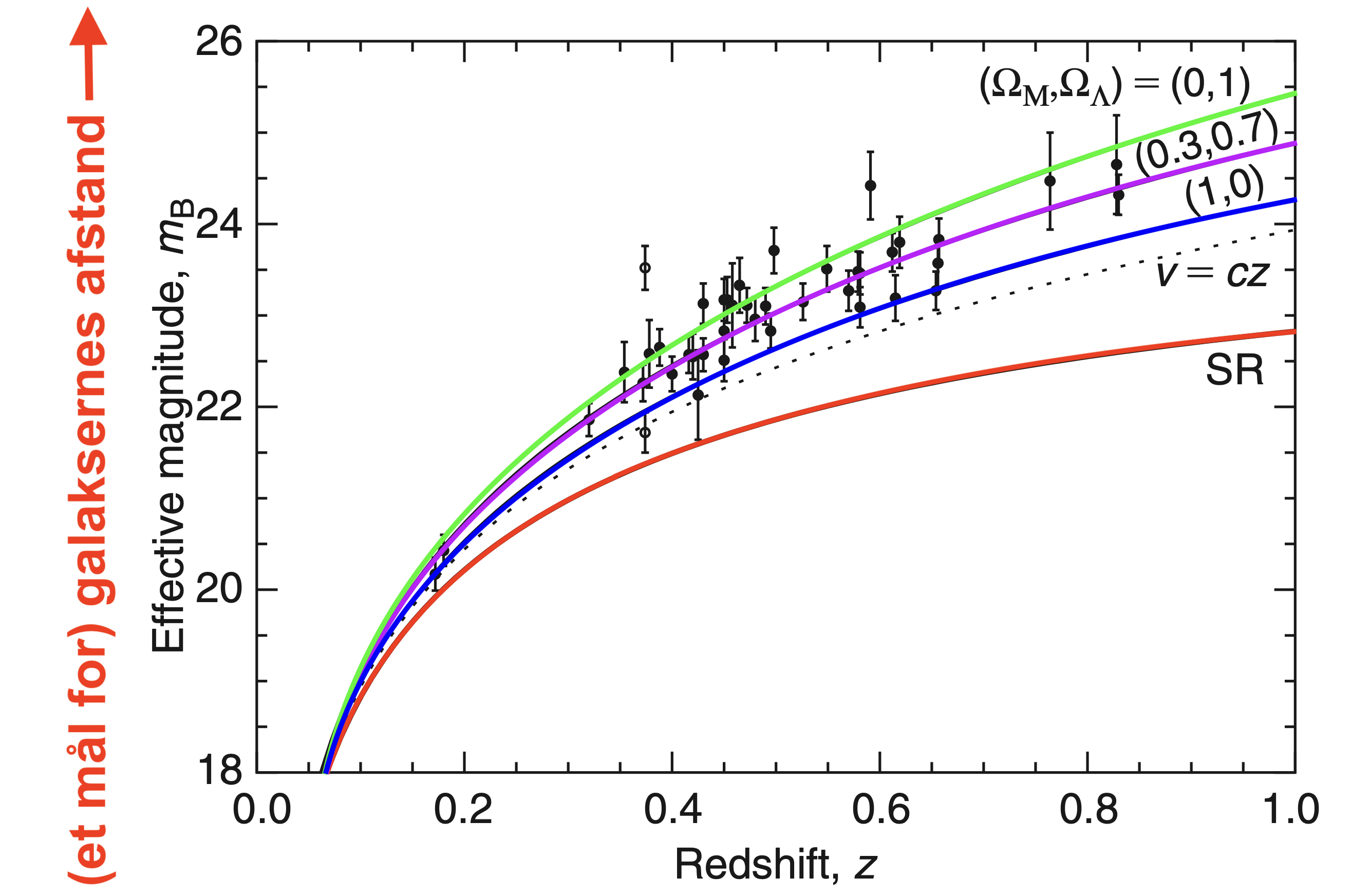
Hvis denne sammenhæng skyldtes at de bevægede sig gennem rummet, forudsiger speciel relativitetsteori, at de burde ligge omkring den røde linje. Hvis sammenhængen derimod skyldtes at lyset bevægede sig gennem et ekspanderende rum, forudsiger generel relativitetsteori, at de burde ligge omkring den blå linje (hvis Universet kun indeholdt stof), den grønne linje (hvis Universet kun indeholdt mørk energi), og den lilla linje (hvis Universet indeholder et mix af ca. 30% stof og 70% mørk energi).
Den lilla linje giver det bedste fit, og selvom man kan diskutere det præcise forhold mellem stof og mørk energi, er det tydeligt, at denne beskrivelse passer langt, langt bedre end SR's Doppler-forskydning. Med flere og flere data, samt andre måder at måle på, har vi efterhånden ret godt styr på, hvad og hvor meget Universet indeholder. Kredit: Davis & Lineweaver (2004).
Svaret
Og nu er jeg så klar til at besvare dit spørgsmål:
Præcis hvordan, og hvor hurtigt, Universet udvider sig nu og i fortiden og i fremtiden er én af de fornemste opgaver at løse indenfor kosmologi. Vi er efterhånden kommet så langt, at vi kan beskrive denne udvidelse temmelig nøjagtigt gennem hele Universets historie. Når vi kigger på en galakse og måler rødforskydningen af dens lys, ved vi derfor
- Hvor hurtigt den bevæger sig væk fra os nu;
- Hvor hurtigt den bevægede sig væk fra os, dengang den udsendte dét lys, vi ser i dag;
- Hvor langt væk den er i dag, og dengang den udsendte lyset;
- Hvor lang tid, lyset har været undervejs (dvs. hvor mange år vi kigger tilbage i tiden);
- Hvor gammelt Universet var dengang;
og hvordan forskellige andre fysiske forhold var dengang, f.eks. Universets tæthed og temperatur dengang dengang.
Universets udvidelse er beskrevet matematisk ved "Hubbles lov" (som også er en del af ΛCDM-modellen). Denne lov siger, at hastigheden (\(v\)) hvormed en galakse fjerner sig fra en anden galakse er proportional med afstanden (\(d\)) mellem dem. Sådan her: $$ v = H \, \times \, d. $$ Hvis G2 er dobbelt så langt væk som G1 betyder det altså, at G2 bevæger sig dobbelt så hurtigt væk fra os som G1. Og dét er uanset hvilken retning de galakser ligger i. Proportionalitets-faktoren \(H\) kaldes "Hubble-konstanten", og måles i "hastighed per afstand". Den er konstant i hele Universet; altså Universet udvider sig på samme måde over det hele (så vidt vi kan se, men det behøver ret beset ikke være sådan).
Normalt angiver vi \(H\) i kilometer i sekundet, per "Mega-parsec". Én parsec er ca. 3.3 lysår, så en Mega-parsec (eller "Mpc") er altså 3.3 millioner lysår. \(H\)'s værdi i dag kalder vi \(H_0\) (H-nul), og dens værdi er ca. 70 km/s/Mpc, eller ca. 21.5 km/s per mega-lysår.
Med andre ord: De to galakser G1 og G2 ligger hhv. 1 og 2 mia. lysår (eller 1000 og 2000 mega-lysår) væk, og vi ved derfor, at de — netop nu — bevæger sig væk fra os med med hhv. 21.500 og 43.000 km/s.
Vores model fortæller os også, at dengang de to galakser udsendte dét lys vi ser i dag, fjernede de sig med hhv. 20.700 km/s og 40.200 km/s. De bevæger sig altså lidt hurtigere væk i dag, men hvordan deres hastighed har ændret sig gennem tiden, er ikke helt trivielt at beregne. Det kræver, at man integrerer den såkaldte "Friedmann-ligning", som er en af de ligninger, som ΛCDM-modellen hviler på.
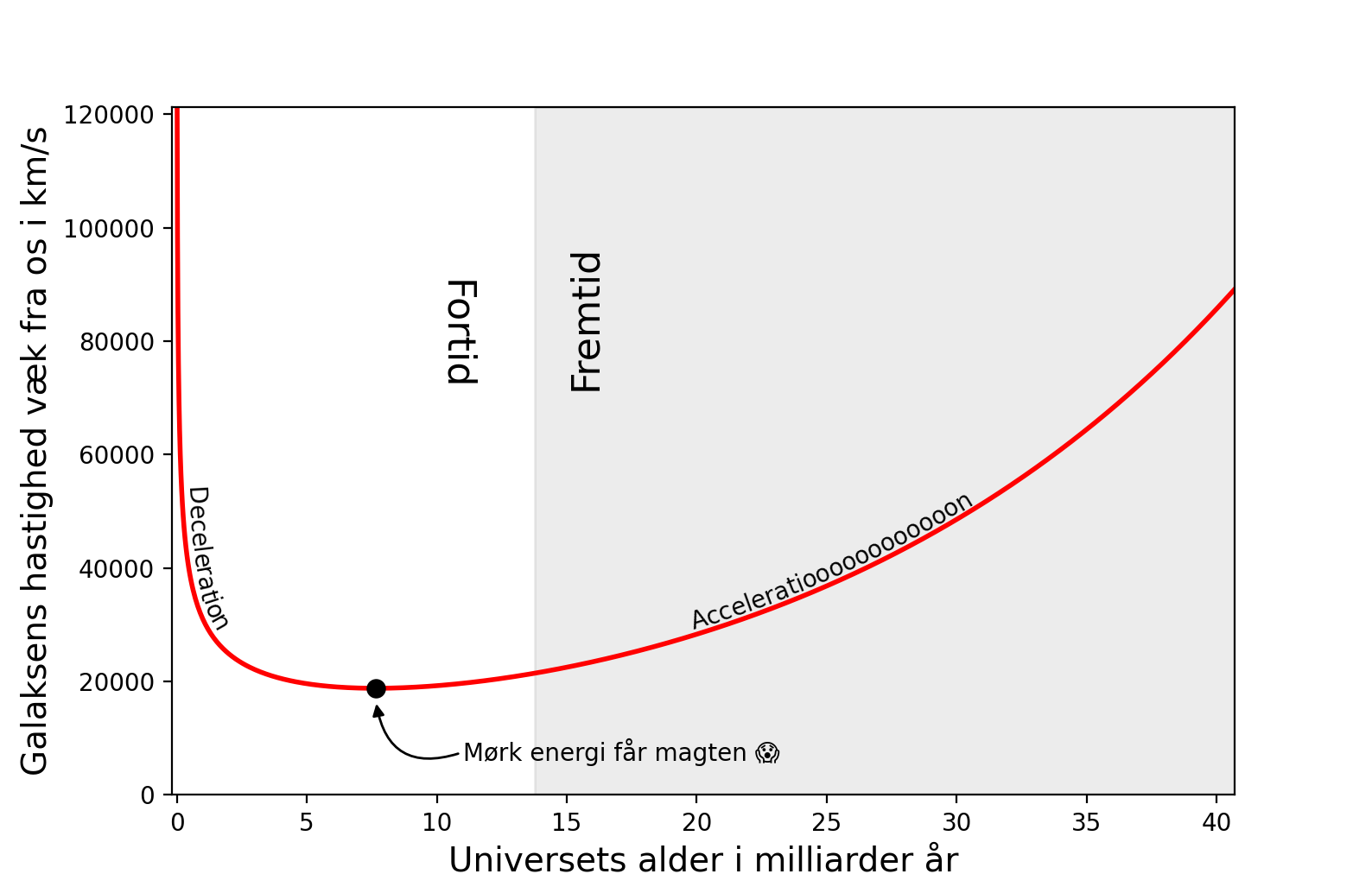
Som en lille service har jeg løst ligningen for dig. På den første figur her kan du se, hvordan galaksen G1's hastighed har været gennem tiden.
For eksempel kan du se, at galakser i starten af Universets levetid fjernede sig langsommere og langsommere fra hinanden. Dette skyldes simpelthen deres indbyrdes tyngdekraft. Men på et tidspunkt begyndte Universets dynamik at blive domineret af den mørke energi, som har den modsattte effekt at accelerere udvidelsen.
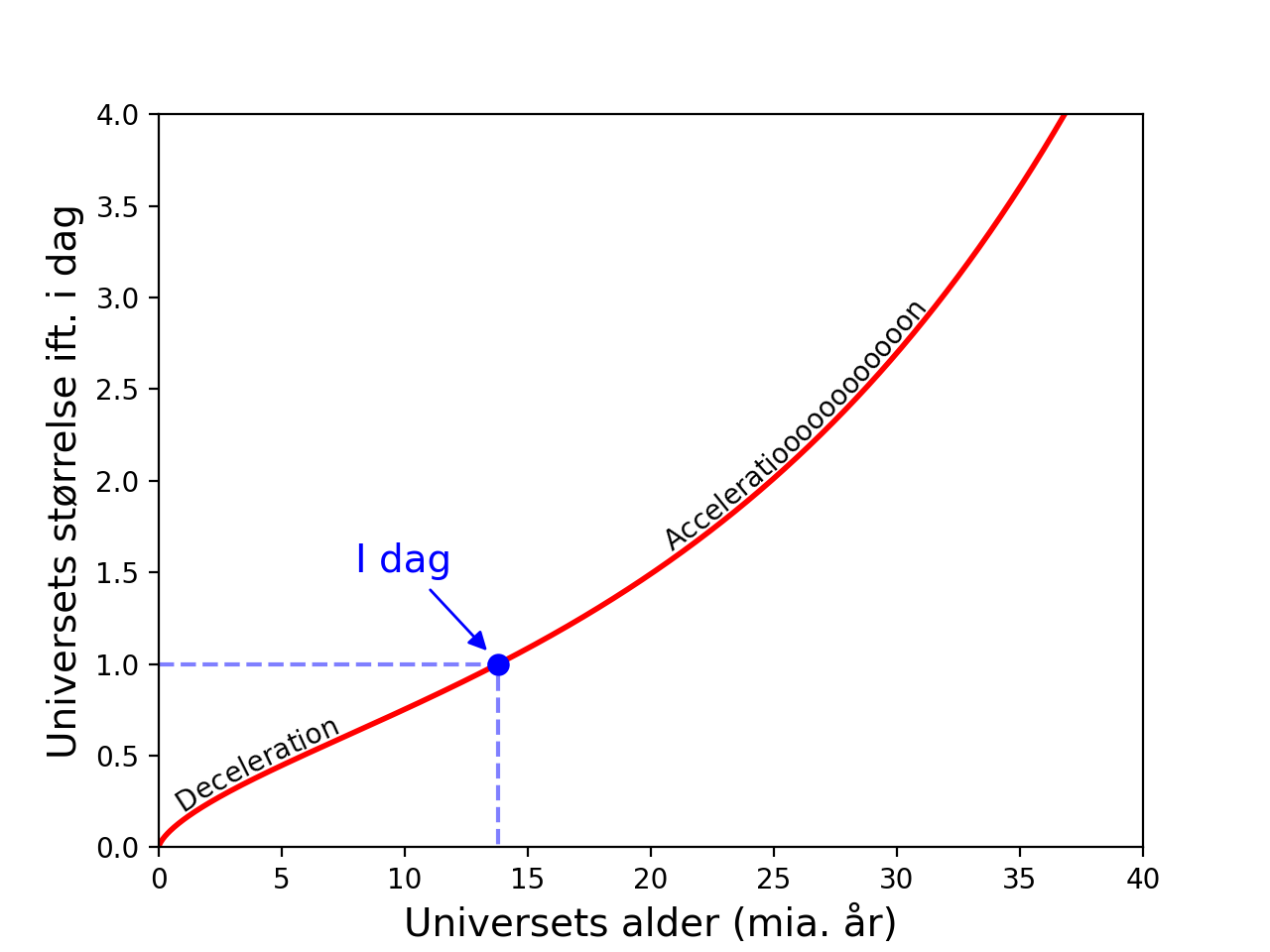
På den anden figur kan du se, hvordan Universets størrelse har ændret sig gennem tiden, altså hvordan udvidelsen er foregået. Vi ved ikke, om Universet er endeligt eller uendeligt, så "størrelsen" er defineret til at være lig med "1" i dag. For eksempel kan du se, at det var halvt så stort (dvs. alle galakser halvt så langt fra hinanden), dengang Universet var godt 6 mia. år gammelt. Og om 23 mia. år, når Universet er knap 37 mia. år gammelt, vil galakserne være 4 gange så langt fra hinanden.