Quick explanation
Lyman α radiation is a kind of ultraviolet light coming from hydrogen.
It is emitted especially from gas around massive stars, and is a rich source of information about galaxies.
After the first few paragraphs, this article goes somewhat beyond a layman's explanation, directed more toward students or teachers of astrophysics, who would like to have a basic understanding of Lyman α (I don't think it's completely incomprehensible to non-astronomers, though).
If you're just here for the movies, you may go directly to the last section. Here's an overview of the sections:
Lyman α is light
Most of the information we receive from space comes to us in the form of electromagnetic radiation, also known as light. Radiation consists of light particles, or photons, which are small packets of energy.
The higher the energy, the higher the frequency, but the shorter the wavelength, and vice versa. The different terms are just different ways of talking about the light. Sometimes — especially when the wavelength is long — it makes more sense to think of light as waves.
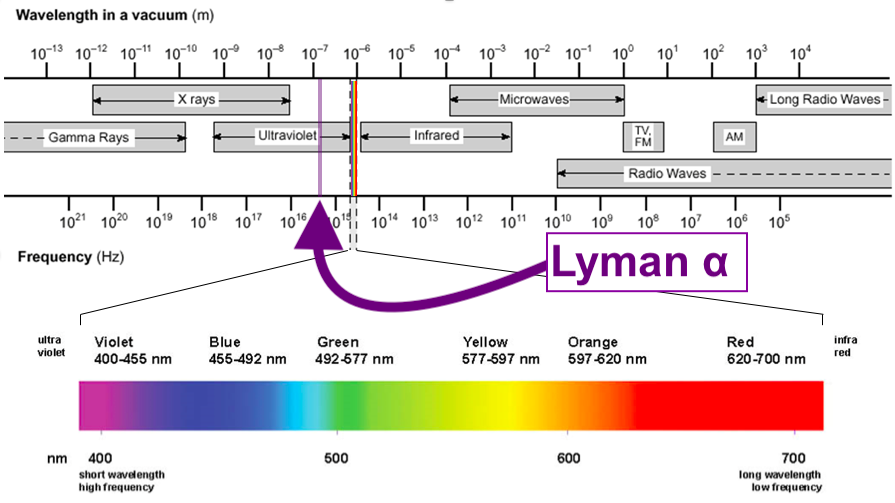
Astronomers often like to measure wavelengths in Ångström ("Å"), which is a 100 millionth of a cm. Or a tenth of a nanometer. If the wavelength lies between approximately 4000 Å and 7000 Å, the light is visible to the human eye.
The shorter the wavelength, the more blue the light is, while it becomes more red for longer wavelengths. When its shorter than 4000 Å, we call it ultraviolet (UV) light, and for even shorter wavelengths we have X-rays and gamma rays. Above 7000 Å, we call it infrared, microwaves, and radiowaves. Together, all these photons comprise a spectrum of light.
One special type of UV light is particularly interesting in astronomy… to some astronomers… to me,
namely photons with a wavelength of 1216 Å. Radiation consisting of photons
with this wavelength is called "Lyman α radiation", or simply Lyα.
Lyman α is emitted from hydrogen (in galaxies)
Lyman α is light from hydrogen atoms. For reasons that are explained further below, Lyα is abundantly produced in galaxies in particular during their formation. On the way out of the galaxy, and through the intergalactic medium, the Lyα spectral line is reshaped according to the physical conditions governing the galaxy. While this makes the interpretation of the line notoriously difficult, it is also an essential key to learning about the galaxies.
The intensity and the exact shape of the spectral line profile reflect properties such as the galaxy's star formation rate, gas temperature and density, dust contents, as well as turbulence, kinematics, and outflows — quantities that characterize a galaxy.
Since Lyα is in the UV range, although it may travel billions of light-years through the Universe, it is almost entirely absorbed by our atmosphere. However, for very distant galaxies the cosmological redshift converts it into visible or infrared light, which easily penetrates the atmosphere.
Hence, Lyα is one of our main windows to, in particular, the very distant Universe. Since the very distant Universe also means the very early Universe, observations of Lyα radiation is a fantastic tool to learn about how the galaxies formed.
And galaxies are pretty cool.
Click image to animate.
How is Lyman α produced?
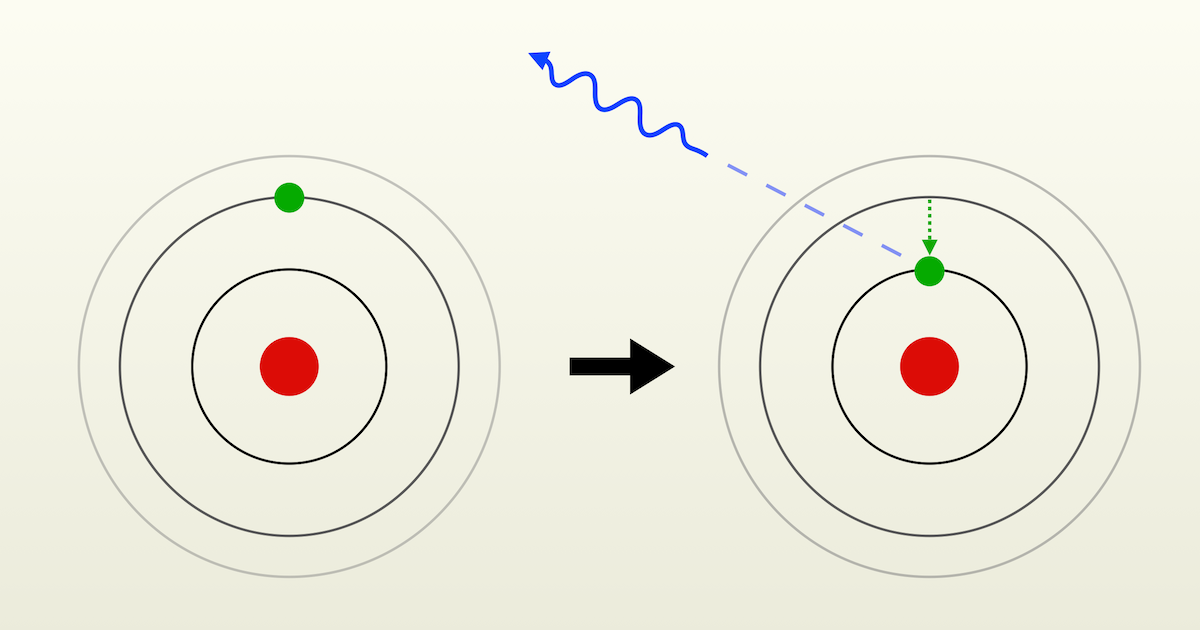
As decribed above, Lyα is emitted when an electron in a neutral hydrogen atom jumps from the first excited state to the ground state. But how does the electron get to the upper level in the first place?
Since the energy difference between the two states equals the energy of a Lyα photon, one way is that it has absorbed another Lyα photon. But then we may ask "Where did that photon come from?"
There are basically two different ways to produce Lyα — through ionization and subsequent recombination, or through collisional excitation. These processes are described below.
Ionization and recombination
If the hydrogen atom is ionized — i.e. it doesn't have an electron at all — it will be positively charged (it will then just be a free proton). If the gas density is not too low, and if the temperature is not too high, it will eventually meet and capture a free electron.
The electron may go directly to the ground state, emitting a high-energy photon (which later is able to ionize another hydrogen atom). But it may also go to one of the excited state. If it goes to the 1st state, it will then decay to the ground state, emitting a Lyα photon. If it goes to one of the higher states, it will decay possibly through several intermediate states, which may or may not involve the 1st state. This process is called cascading.
It turns out that each time a proton and an electron recombine, they have roughly 2/3 chance of emitting a Lyα photon.
Click image to animate.
Collisional excitation
The other way to get the electron in the first excited state is through collisions. If a neutral hydrogen atom collides with another particle (usually an electron), the electron may be bumped to an excited state, which — as in the case with recombinations — will result in the subsequent emission of one or more photons, usually involving a Lyα photon.
That is, the kinetic energy of the particles is converted into radiation which can escape, removing energy from the gas. In other words, the gas cools. Hence, this process is also called cooling radiation.
For this process to be important, the temperature can't be too low, since the particles won't have enough energy to excite the electron. But it also can't be too high, because then most of the gas is ionized, plus the increased pressure makes the density too low for the particles to meet often enough. For this reason, Lyα cooling radiation is most efficient when the gas temperature is the range 104–105 K.
Click image to animate.
Lyα from forming galaxies
Stars
When galaxies form, they usually go through a period of intense star formation. The most massive stars — the so-called O and B stars — burn fast, live short, and are very bright in the ultraviolet.
Hence they're able to ionize the neutral gas around them. When the gas recombines, Lyα is emitted in copious amounts.
Since almost all of the ionizing radiation is absorbed, this means that 2/3 of the entire spectrum blueward of the ionization threshold at 912 Å is converted into a single, narrow emission line. This phenomenon can make young, starbursting galaxies extremely bright when observed in Lyα.
Cooling
The other process, collisional excitation, may help to make them even more bright. Galaxies form from gigantic clouds of gas and dark matter collapsing under its own gravity. In order to settle down and form a galaxiy, the gas has to cool. In some circumstances, especially in the early Universe, this cooling happens at low enough temperatures that the cooling happens mainly by emission of Lyα.
Although the Lyα due to star formation will usually dominate, a significant fraction of the emitted Lyα could come from cooling radiation. And if the galaxy is very dusty, most of the "stellar" Lyα may be absorbed (since dust is close to the stars) while the cooling Lyα is typically emitted farther away from the dusty regions.
Click image to animate.
Lyα radiative transfer
Radiative transfer is the calculation of how light propagates through a medium, e.g. how much is light absorbed as it travels through a dusty cloud.
For Lyα, such calculations are particularly difficult. The reason is that Lyα is a resonant line: Its energy corresponds exactly to the energy difference between the ground state of the first excited state. Hence, a Lyα photon is not just absorbed by a hydrogen atom — it is re-emitted almost immediately, but in another direction. This process is called resonant scattering.
Diffusion in space
That means that a Lyα photon created deep inside a star-forming region in a galaxy makes a "random walk" out through the neutral gas before it can escape the galaxy. And this in turn means that the direction in which Lyα is observed is not in general the direction from which it was emitted.
For instance, although star-forming clouds may occupy small regions of a galaxy, Lyα may not escape until large distance from the center, resulting in the galaxy being surrounded by a Lyα halo. In other words, a Lyα-emitting galaxy may look much larger when observed in Lyα than when observed in other wavelengths.
Moreover, unless the galaxy is close to spherical, it will be easier for the Lyα to escape in some direction than other. Hence, depending on which direction we observe the galaxy from, it may be very bright or close to black.
Credit: Östlin et al. (2014).
Diffusion in wavelength
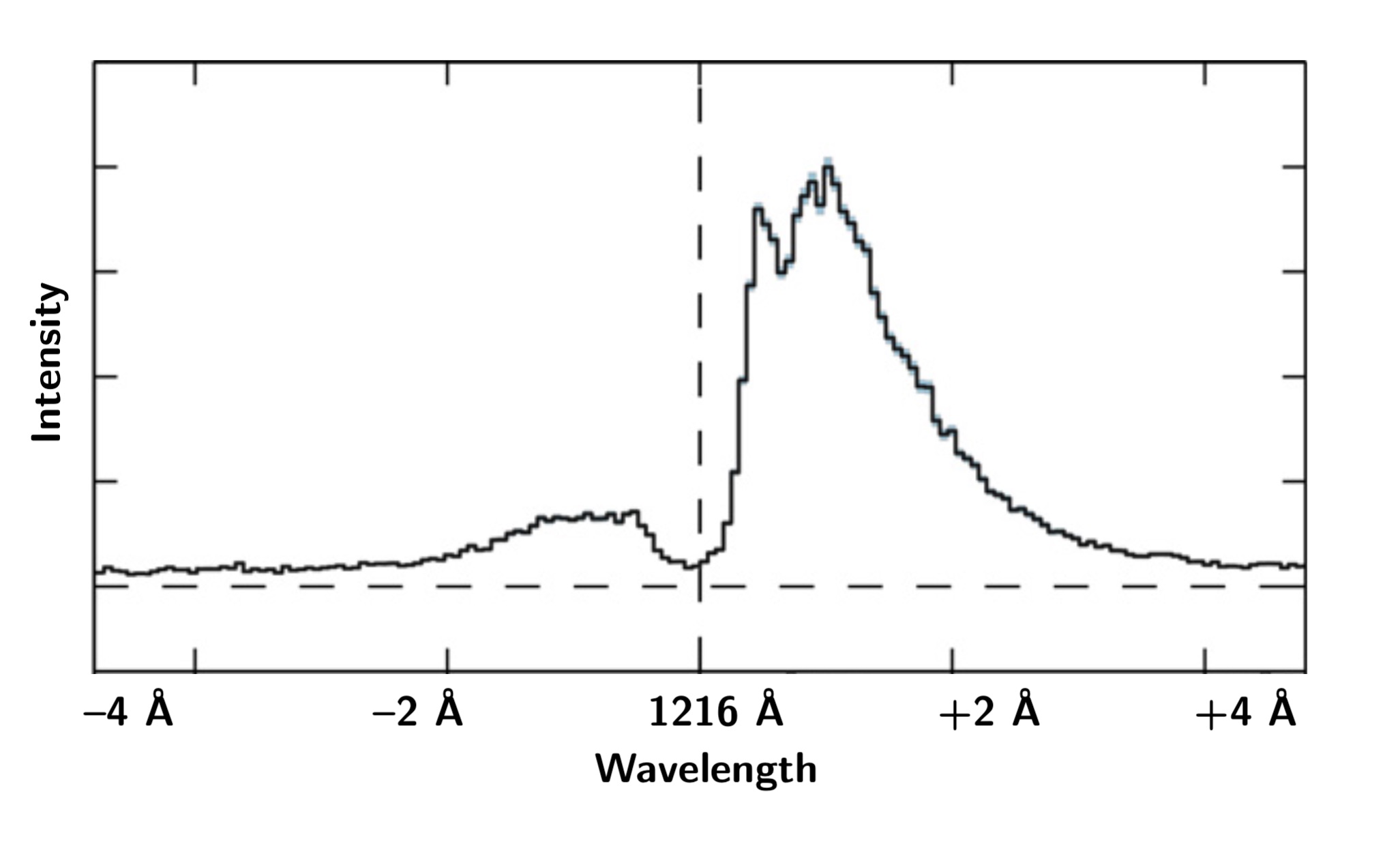
And as if this was not enough, each of the thousands or millions of scatterings changes the photon's wavelength a little bit. But how can this be? The energy of the photon before and after the sacttering should be the same, right?
Not exactly! The probability of a photon interacting with an atom depends strongly on its exact wavelength. If the photon has a wavelength of exactly 1215.67 Å, the probability is highest (yes I know I said "1216 Å" before, but I rounded off). If it's just slightly shorter, say 1215.59 Å, the probability is ten times smaller, and if the wavelength is 1214.82 Å, the probability is a million times smaller.
However, if the atom is moving away from the photon, then in the reference frame of the atom, the photon will be Doppler-shifted. If the photon's wavelength is 1215.59 Å, a velocity of roughly 20 km/s is needed to redshift it to 1215.67 Å, increasing its probability of being scattered ten times. For the 1214.82 Å photon, a velocity of some 200 km/s is needed (such a velocity is not unlikely in the interstellar medium of a galaxy).
When the photon then is re-emitted, it will acquire a second Doppler shift from the component of the atom's velocity in the direction of the scattering. If the photon is scattered roughly perpendicular to the motion of the atom, there will be close to no Doppler shift, and the photon will hence have changed its wavelength from 1215.59 Å to roughly 1215.67 Å. And if the photon happens to be scattered back into the direction where it came from, it will be redshifted to roughly 1215.75 Å.
Thus, the radiative transfer of Lyα involves diffusion in both space and wavelength. As the probability of being scattered decreases quickly with wavelength-distance from the central wavelength of 1215.67 Å, the archetypical spectrum of a Lyα-emitting galaxy is double-peaked around 1215.67 Å, with the intensity between the peaks being zero.
Click image to animate.
Credit: Rivera-Thorsen et al (2015).
Numerical radiative transfer
Because of these complications, only in a few, idealized cases is it possible to calculate analytically ("with pen and paper") the radiative transfer of Lyα. These idealized cases usually assume that the galaxy is homogeneous (i.e. a smooth distribution of gas), isotropic (i.e. symmetric about the center), isothermal (i.e. has the same temperature everywhere), and static (i.e. no large-scale motions).
Although one may learn a lot from such considerations, galaxies are not really like this: Rather they are clumpy and anisotropic, and gas cloud move around with large velocities, especially in outflows, i.e. when gas is blown out of the galaxies due to feedback from stellar activity and active galactic nuclei.
In other words, real galaxies are a mess.
Simulating a galaxy
Luckily, with the aid of computers we are still able to learn how Lyα propagates the interstellar medium of realistic galaxies and make its way down to our telescopes. This is great, because then we can predict what we will observe, and we can interpret what we have observed (that's basically what I do for a living).
The basic idea is as follows:
First you make a galaxy in your computer. Either you define it as a simplified shape (e.g. spherical with two outflowing jets and some amount of clumpiness), or you simulate it in a hydrodynamic, cosmological simulation.
The first case is simple and idealized, but has the advantage that the physical parameters describing it may be defined as you wish. The second case has the advantage of being much more realistic (simulated galaxies really look like real galaxies), at the price that you have much less influence on how a given galaxy will look.
Monte Carlo simulations
In any case you can then describe, in your computer, a galaxy by a number of physical parameters — such as hydrogen density, temperature, velocity field, and dustiness — in every point in space. Typically this is done by splitting up space in little cells (3D pixels). The more cells, the better the resolution. You can even refine some cells into eight subcells, refine some subcells in to sub-subcells, and so on.
Then you emit Lyα photons from the luminous regions in the galaxy, in random directions, one at a time. Each photon is traced as it scatters its way on hydrogen atom after hydrogen atom, through cell after cell, all the time changing its direction and wavelength, until eventually it escapes the galaxy in some direction (or meets its doom on the surface of a dust grain).
The velocity of a given scattering atom, and the direction into which a given photon is scattered, are random, found by using a "random number generator". This has given the technique its name, Monte Carlo simulations.
After having traced thousands or millions of photons you eventually have enough statistics to say how the galaxy and it spectrum looks in different directions.
Dig deeper…
If you want more details on the theoretical (and some observational) aspects of Lyman α, I've been told that my Ph.D. thesis is quite pedagogical:
Laursen (2010): Interpreting Lyman α radiation from young, dusty galaxies.
Downloads
Here you can download the animations from this article (in low- or high-res), or the Keynote slides in which I made the animations. You're free to use them in talks and teaching, or just watch them every night before you go to sleep. You're also free to modify them, distribute them, and use them commercially (if you can find any way to do that).
If someone asks where you got them, I'd appreciate if you'll acknowledge me :)